Related Articles
- 1 Evaluate a Decision Tree Model
- 2 Future Value vs. Present Value
- 3 Decision Evaluation Tools
- 4 In What Ways Can Decision Trees Be Used for Business Decisions?
Business owners have to make decisions every day on issues fraught with uncertainty. Information is not perfect, and the best choice is not always clear. One way to handle these vague situations is to use a decision tree. Decision trees have numerous advantages that make them useful tools for managers.
What Is a Decision Tree?
The adjective 'decision' in 'decision trees' is a curious one and somewhat misleading. In the 1960s, originators of the tree approach described the splitting rules as decision rules. The terminology remains popular. This is unfortunate because it inhibits the use of ideas and terminology from 'decision theory'.
A decision tree is a managerial tool that presents all the decision alternatives and outcomes in a flowchart type of diagram, like a tree with branches and leaves. Each branch of the tree represents a decision option, its cost and the probability that it is likely to occur. The leaves at the end of the branches show the possible payoffs or outcomes. A decision tree illustrates graphically all the possible alternatives, probabilities and outcomes and identifies the benefits of using decision analysis.
How Does a Decision Tree Work?
Let's start with a simple example, and explain how decision trees are used to value investment alternatives. Suppose you are trying to decide between starting two types of businesses: a lemonade stand or a candy store.
The candy store has the potential to earn up to $150; the lemonade stand could earn a maximum of $120. At this point, the answer is obvious. Go with the candy store because it can earn more than the lemonade stand.
But starting a business and making a profit is never a sure thing. The candy store has a 50 percent chance of success and a 50 percent chance of failure. If it succeeds, you would make $150. On the other hand, if it fails, you would lose your startup costs of $30.
However, the weather is hot, and the lemonade stand has a 70 percent chance of success and a 30 percent possibility of failure. If it works, you would make $120; if not, you lose the initial investment of $20.
Now, which business do you choose? The answer can be found by using the decision tree format and the concept of 'expected value.'
Differential Diagnosis Decision Tree
Mathematically, expected value is the projected value of a variable found by adding all possible outcomes, with each one multiplied by the probability that it will occur. This sounds murky, but it will be clearer with our example.
Let's calculate the expected value of investing in the candy store. The formula is as follows:
- Expected value-candy = 50 percent X outcome of success + 50 percent x outcome of failure.
- Expected value-candy = 0.50 x $150 + 0.50 x (-$30) = $60.
Now, calculate the expected value of the lemonade stand.
- Expected value-lemonade = 70 percent X outcome of success + 30 percent x outcome of failure.
- Expected value-lemonade = 0.70 X $120 + 0.30 X (-$20) = $78.
Since the objective is to choose the business that will probably earn the most money, this analysis shows that the lemonade stand is the best choice. It has a higher expected value of $78 versus the $60 expected value of the candy store.
How to Use a Decision Tree With Information
Now, let's look at the advantages of using a decision tree to solve a more complex problem.
Say you're a manufacturer of a stainless steel part that goes into a washing machine, and you are facing a decision. Do you fabricate this part in your existing facilities or do you subcontract it out to another machine shop?
All sorts of uncertainties exist around this decision, and the decision must be made before knowing the strength of the economy and the level of demand.
Following is the data needed to construct a decision tree for this situation. Figures are in thousands of dollars.
We have three economic conditions: strong economy with high demand , medium economy or a weak economy with low demand.
The probability of occurrence for each demand level is: 0.30 for high, 0.40 for medium and 0.30 for low.
If the product is fabricated in-house, the return is $200 for high demand, $60 for medium and a loss of $30 for low. The reason for the negative return on low demand is that it costs money to set up the equipment for in-house fabrication, and if the demand is not high enough to cover these setup costs, the result is a loss.
The returns for purchasing from an outside supplier are $140 if demand is high, $80 for medium demand and $20 when demand is low.
The cost for hiring an economic consultant to get advice on the direction of the economy is $10. The probability that the consultant will predict a favorable economy is 0.40 and 0.60 for an unfavorable one. Note that these probabilities will change the original assumed probabilities without benefit of the research.
The decision objective has two parts: Determine whether to pay for the market research and decide on the best strategy.
After constructing the decision tree with all the probabilities and expected payoffs, we find that the expected value after paying for the market research is $74.6 However, the expected value without the market research is $80.
In this case, conducting the research results in a lower expected value, $74.6 versus $80, so the decision is not to hire the consultant for the research.
Now, we have to decide whether to fabricate the part in-house or sub it out.
The decision tree starts out with two branches: Hire the consultant or not hire.
Each of these two branches lead to decision nodes with more branches for manufacture in-house or sub the work out. At the end of all these branches are the leaves, which represent the payoffs for each of the three economic conditions.
After putting in all of the probabilities and payoffs, the decision tree shows that the expected value for using the consultant is $75, and the expected value for not using the consultant is $80. The expected value for not using the consultant is higher, so that choice is selected.
Going one step further, the decision tree shows a higher expected value for contracting the work out, so the manufacturer hires the outside supplier.
Without going into the mathematical details, we can see the advantages of a decision tree as a useful tool to find solutions to problems that have a myriad of probabilities and expected payoffs. Decision trees provide a rational way to choose between different courses of action.
Using a Decision Tree For Predicting Outcomes
In addition to using decision trees to choose alternatives based on expected values, they can also be used for classification of priorities and making predictions.
An example will best explain this application. Suppose a watch retailer wants to know the likelihood that an online customer will purchase a watch. A decision tree can be constructed that shows the attributes of this situation: gender, age and level of income.
A decision tree will identify which of these attributes has the highest predictive value and, ultimately, whether the visitor to the company's website will make a purchase.
Examples of Applications for Decision Trees
Using decision trees to decide on courses of action using expected values have common applications like the following:
- The CFO is deciding whether to invest $10,000 in excess cash in stock or leave in a bank savings account based on future expectations of the economy.
- A farmer using rainfall forecasts, predictions of commodity prices and yields per acre to decide between planting soybeans, corn or collecting a government subsidy by not planting anything.
- An owner of a successful pizzeria is trying to decide whether to expand the existing store or open another one in a nearby town.
- A romance novel author is considering offers for one of her popular novels from a movie company and also from a TV network. The amount that the movie company will pay varies with the box office attendance, whereas the TV network is a flat, upfront payment. Which offer to accept?
- The company is considering leasing cars for all sales staff, purchasing the cars or paying employees for business miles in their own cars.
These are examples of classification problems that can be analyzed using decision trees:
- Categorizing a customer bank loan application on such factors as income level, years on present job, timeliness of credit card payments and existence of a criminal record.
- Deciding whether or not to play tennis based on historical data of forecast (sunny, overcast or rainy), temperature (hot, mild or cool), humidity (high or normal) and wind speeds (windy or not).
- Prioritizing patients for emergency room treatment based on age, gender, blood pressure, temperature, heart rate, severity of pain and other vital measurements.
- Using demographic data to determine the effect of a limited advertising budget on the number of likely buyers of a certain product.
What Are the Advantages of Decision Tree Analysis?
Decision trees have a number of advantages as a practical, useful managerial tool.
Comprehensive
A significant advantage of a decision tree is that it forces the consideration of all possible outcomes of a decision and traces each path to a conclusion. It creates a comprehensive analysis of the consequences along each branch and identifies decision nodes that need further analysis.
Specific
Decision trees assign specific values to each problem, decision path and outcome. Using monetary values makes costs and benefits explicit. This approach identifies the relevant decision paths, reduces uncertainty, clears up ambiguity and clarifies the financial consequences of various courses of action.
When factual information is not available, decision trees use probabilities for conditions to keep choices in perspective with each other for easy comparisons.
Easy to Use
Decision trees are easy to use and explain with simple math, no complex formulas. They present visually all of the decision alternatives for quick comparisons in a format that is easy to understand with only brief explanations.
They are intuitive and follow the same pattern of thinking that humans use when making decisions.
Versatile
A multitude of business problems can be analyzed and solved by decision trees. They are useful tools for business managers, technicians, engineers, medical staff and anyone else who has to make decisions under uncertain conditions.
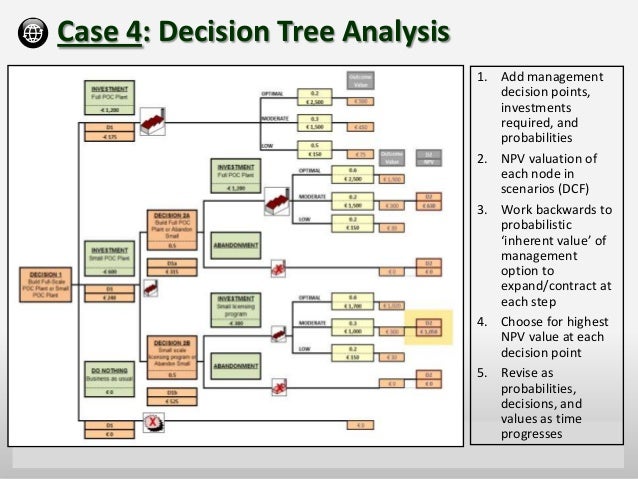
The algorithm of a decision tree can be integrated with other management analysis tools such as Net Present Value and Project Evaluation Review Technique (PERT).
Simple decision trees can be manually constructed or used with computer programs for more complicated diagrams.
Decision trees are a common-sense technique to find the best solutions to problems with uncertainty. Should you take an umbrella to work today? To find out, construct a simple decision-tree diagram.
References (6)
About the Author
James Woodruff has been a management consultant to more than 1,000 small businesses. As a senior management consultant and owner, he used his technical expertise to conduct an analysis of a company's operational, financial and business management issues. James has been writing business and finance related topics for work.chron, bizfluent.com, smallbusiness.chron.com and e-commerce websites since 2007. He graduated from Georgia Tech with a Bachelor of Mechanical Engineering and received an MBA from Columbia University.
Cite this ArticleChoose Citation Style
Abstract
Background
New technologies like echocardiography, color Doppler, CT, and MRI provide more direct and accurate evidence of heart disease than heart auscultation. However, these modalities are costly, large in size and operationally complex and therefore are not suitable for use in rural areas, in homecare and generally in primary healthcare set-ups. Furthermore the majority of internal medicine and cardiology training programs underestimate the value of cardiac auscultation and junior clinicians are not adequately trained in this field. Therefore efficient decision support systems would be very useful for supporting clinicians to make better heart sound diagnosis. In this study a rule-based method, based on decision trees, has been developed for differential diagnosis between 'clear' Aortic Stenosis (AS) and 'clear' Mitral Regurgitation (MR) using heart sounds.
Methods
For the purposes of our experiment we used a collection of 84 heart sound signals including 41 heart sound signals with 'clear' AS systolic murmur and 43 with 'clear' MR systolic murmur. Signals were initially preprocessed to detect 1st and 2nd heart sounds. Next a total of 100 features were determined for every heart sound signal and relevance to the differentiation between AS and MR was estimated. The performance of fully expanded decision tree classifiers and Pruned decision tree classifiers were studied based on various training and test datasets. Similarly, pruned decision tree classifiers were used to examine their differentiation capabilities. In order to build a generalized decision support system for heart sound diagnosis, we have divided the problem into sub problems, dealing with either one morphological characteristic of the heart-sound waveform or with difficult to distinguish cases.
Results
Relevance analysis on the different heart sound features demonstrated that the most relevant features are the frequency features and the morphological features that describe S1, S2 and the systolic murmur. The results are compatible with the physical understanding of the problem since AS and MR systolic murmurs have different frequency contents and different waveform shapes. On the contrary, in the diastolic phase there is no murmur in both diseases which results in the fact that the diastolic phase signals cannot contribute to the differentiation between AS and MR.
We used a fully expanded decision tree classifier with a training set of 34 records and a test set of 50 records which resulted in a classification accuracy (total corrects/total tested) of 90% (45 correct/50 total records). Furthermore, the method proved to correctly classify both AS and MR cases since the partial AS and MR accuracies were 91.6% and 88.5% respectively. Similar accuracy was achieved using decision trees with a fraction of the 100 features (the most relevant). Pruned Differentiation decision trees did not significantly change the classification accuracy of the decision trees both in terms of partial classification and overall classification as well.
Discussion
Present work has indicated that decision tree algorithms decision tree algorithms can be successfully used as a basis for a decision support system to assist young and inexperienced clinicians to make better heart sound diagnosis. Furthermore, Relevance Analysis can be used to determine a small critical subset, from the initial set of features, which contains most of the information required for the differentiation. Decision tree structures, if properly trained can increase their classification accuracy in new test data sets. The classification accuracy and the generalization capabilities of the Fully Expanded decision tree structures and the Pruned decision tree structures have not significant difference for this examined sub-problem. However, the generalization capabilities of the decision tree based methods were found to be satisfactory. Decision tree structures were tested on various training and test data set and the classification accuracy was found to be consistently high.
Background
New technologies like Echocardiography, Color Doppler, CT, and MRI provide more direct and accurate evidence of heart disease than heart auscultation. However, these modalities are costly, large in size and operationally complex []. Therefore these technologies are not suitable for use in rural areas, in homecare and generally in primary healthcare set-ups. Although heart sounds can provide low cost screening for pathologic conditions, internal medicine and cardiology training programs underestimate the value of cardiac auscultation and junior clinicians are not adequately trained in this field. The pool of skilled clinicians trained in the era before echocardiography continues to age, and the skills for cardiac auscultation is in danger to disappear [2]. Therefore efficient decision support systems would be very useful for supporting clinicians to make better heart sound diagnosis, especially in rural areas, in homecare and in primary healthcare. Recent advances in Information Technology systems, in digital electronic stethoscopes, in acoustic signal processing and in pattern recognition methods have inspired the design of systems based on electronic stethoscopes and computers [3,4]. In the last decade, many research activities were conducted concerning automated and semi-automated heart sound diagnosis, regarding it as a challenging and promising subject. Many researchers have conducted research on the segmentation of the heart sound into heart cycles [5-7], the discrimination of the first from the second heart sound [8], the analysis of the first, the second heart sound and the heart murmurs [9-], and also on features extraction and classification of heart sounds and murmurs [14,15]. These activities mainly focused on the morphological characteristics of the heart sound waveforms. On the contrary very few activities focused on the exploitation of heart sound patterns for the direct diagnosis of cardiac diseases. The research of Dr. Akay and co-workers in Coronary Artery Disease [16] is regarded as very important in this area. Another important research activity is by Hedben and Torry in the area of identification of Aortic Stenosis and Mitral Regurgitation [17]. The reason for this focus on the morphological characteristics is the following: Cardiac auscultation and diagnosis is quite complicated depending not only on the heart sound, but also on the phase of the respiration cycle, the patient's position, the physical examination variables (such as sex, age, body weight, smoking condition, diastolic and systolic pressure), the patient's history, medication etc. The heart sound information alone is not adequate in most cases for heart disease diagnosis, so researchers generally focused on the identification and extraction of the morphological characteristics of the heart sound.
The algorithms which have been utilized for this purpose were based on: i) Auto Regressive and Auto Regressive Moving Average Spectral Methods [5,11], ii) Power Spectral Density [5], iii) Trimmed Mean Spectrograms [18], iv) Sort Time Fourier Transform [11], v) Wavelet Transform [7,9,11], vi) Wigner-Ville distribution, and generally the ambiguous function [10]. The classification algorithms were mainly based on: i) Discriminant analysis [19], ii) Nearest Neighbour [], iii) Bayesian networks [,21], iv) Neural Networks [,8,18] (backpropagation, radial basis function, multiplayer perceptron, self organizing map, probabilistic neural networks etc) and v) rule-based methods [15].
In this paper a rule-based method, based on decision trees, has been developed for differential diagnosis between the Aortic Stenosis (AS) and the Mitral Regurgitation (MR) using heart sounds. This is a very significant problem in cardiology since there is very often confusion between these two diseases. The correct discrimination between them is of critical importance for the determination of the appropriate treatment to be recommended. Previous research activities concerning these diseases were mainly focused on their clinical aspects, the assessment of their severity by spectral analysis of cardiac murmurs [] and the time frequency representation of the systolic murmur they produce [9,22]. The problem of differentiation between AS and MR has been investigated in [3] and [17]. The method proposed in [3] was based on the different statistic values in the spectrogram of the systolic murmurs that these two diseases produce. The method proposed in [17] was based on frequency spectrum analysis and a filter bank envelope analysis of the first and the second heart sound. Our work aims to investigate whether decision tree-based classifier algorithms can be a trustworthy alternative for such heart sound diagnosis problems. For this purpose a number of different decision tree structures were implemented for the classification and differentiation of heart sound patterns produced by patients either with AS or with MR. We chose the decision trees as classification algorithm because the knowledge representation model that they produce is very similar to the differential diagnosis that the clinicians use. In other words this method does not work as a black box for the clinicians (i.e. in medical terms). On the contrary neural networks, genetic algorithms or generally algorithms that need a lot of iteration in order to converge to a solution are working as a black box for the clinicians. Using decision trees clinicians can trace back the model and either accept or reject the proposed suggestion. This capability increases the clinician confidence about the final diagnosis.
In particular, the first goal of this work was to evaluate the suitability of various decision tree structures for this important diagnostic problem. The evaluated structures included both Fully Expanded decision trees Structures and Pruned decision trees Structures. The second goal was to evaluate the diagnostic abilities of the investigated heart sound features for decision tree – based diagnosis. In both the above evaluations the generalization capabilities of the implemented decision tree structures were also examined. Generalization was a very important issue due to the difficulty and the tedious work of having adequate data for all possible data acquisition methods within the training data set. The third goal of this work was to suggest a way of selecting the most appropriate decision tree structures and heart sound features in order to provide the basis of an effective semi-automated diagnostic system.
Problem definition: differentiation between AS and MR murmurs
A typical normal heart sound signal that corresponds to a heart cycle consists of four structural components:
– The first heart sound (S1, corresponding to the closure of the mitral and the tricuspid valve).
– The systolic phase.
– The second heart sound (S2, corresponding to the closure of the aortic and pulmonary valve).
– The diastolic phase.
Heart sound signals with various additional sounds are observed in patients with heart diseases. The tone of these sounds can be either like murmur or click-like. The murmurs are generated from the turbulent blood flow and are named after the phase of the heart cycle where they are best heard, e.g. systolic murmur (SM), diastolic murmur (DM), pro-systolic murmur (PSM) etc. The heart sound diagnosis problem consists in the diagnosis from heart sound signals of a) whether the heart is healthy, or not and b) if it is not healthy, which is the exact heart disease. In AS the aortic valve is thickened and narrowed. As a result, it does not fully open during cardiac contraction in systolic phase, leading to abnormally high pressure in the left ventricle and producing a systolic murmur that has relatively uniform frequency and rhomboid shape in magnitude (Figure (Figure1a).1a). In MR the mitral valve does not close completely during systole (due to tissue lesion) and there is blood leakage back from the left ventricle to the left atrium. MR is producing a systolic murmur that has relatively uniform frequency and magnitude slope (Figure (Figure1b).1b). The spectral content of the MR systolic murmur has faintly higher frequencies than the spectral content of the AS systolic murmur. The closure of aortic valve affects the second heart sound and the closure of the mitral valve affects the first heart sound.
Two heart cycles of AS and MR heart sounds.
It can be concluded by the visual insplection of Figure Figure11 that the AS systolic murmur has very similar characteristics with the MR systolic murmur and therefore the differentiation between these two diseases is a difficult problem in heart sound diagnosis, especially for young inexperienced clinicians. All these facts define the problem of differentiation between the AS and the MR murmurs. In the following sections we propose a method based on time-frequency features and decision tree classifiers for solving this problem.
Methods

Preprocessing of heart sound data
Cardiac auscultation and diagnosis, as already mentioned, are quite complicated, depending not only on the heart sound but also on other factors. There is also a great variability at the quality of the heart sound affected by factors related to the acquisition method. Some important factors are: the type of stethoscope used, the sensor that the stethoscope has (i.e. microphone, piezoelectric film), the mode that the stethoscope was used (i.e. bell, diaphragm, extended), the way the stethoscope was pressed on the patients skin (firmly or loosely), the medication the patient used during the auscultation (i.e. vasodilators), the patient's position (i.e. supine position, standing, squatting), the auscultation areas (i.e. apex, lower left sternal border, pulmonic area, aortic area), the phase of patients' respiration cycle (inspiration, expiration), the filters used while acquiring the heart sound (i.e. anti-tremor filter, respiratory sound reduction, noise reduction). The variation of all these parameters leads to a large number of different heart sound acquisition methods. A heart sound diagnosis algorithm should take into account the variability of the acquisition method, and also be tested in heart sound signals from different sources and recorded with different acquisition methods. For this purpose we collected heart sound signals from different heart sound sources [31-39] and created a 'global' heart sound database. The heart sound signals were collected from educational audiocassettes, audio CDs and CD ROMs and all cases were already diagnosed and related to a specific heart disease. For the purposes of the present experiment 41 heart sound signals with 'clear' AS systolic murmur and 43 with ' 'clear' MR systolic murmur were used.
This total set of 41 + 43 = 84 heart sound signals were initially pre-processed in order to detect the cardiac cycles in every signal, i.e. detect S1 and S2, using a method based on the following steps:
a) Wavelet decomposition as described in [7] (with the only difference being that the 4th and 5th level detail was kept, i.e. frequencies from 34 to 138 Hz).
b) Calculation of the normalized average Shannon Energy [6].
c) A morphological transform action that amplifies the sharp peaks and attenuates the broad ones [5].
d) A method, similar to the one described in [6], that selects and recovers the peaks corresponding to S1 and S2 and rejects the others.
e) An algorithm that determines the boundaries of S1 and S2 in each heart cycle [30].
f) A method, similar to the one described in [8], that distinguishes S1 from S2
In a second phase, every transformed (processed in the first phase) heart sound signal was used to calculate the standard deviation of the duration of all the heart cycles it includes, the standard deviation of the S1 peak value of all its heart cycles, the standard deviation of the S2 peak value of all its heart cycles, and the heart rate. These were the first four scalar features (F1-F4) of the feature vector of the heart sound signal.
In a third phase, the rest of the features were extracted. For this purpose we calculated for each heart sound signal two mean signals for each of the four structural components of the heart cycle, namely two for the S1, two for the systolic phase, two for the S2 and two for the diastolic phase. The first of these mean signals focused on the frequency characteristics of the heart sound; it was calculated as the mean value of each component, after segmenting and extracting the heart cycle components, time warping them, and aligning them. The second mean signal focused on the morphological time characteristics of the heart sound; it was calculated as the mean value of the normalized average Shannon Energy Envelope of each component, after segmenting and extracting the heart cycles components, time warping them, and aligning them. Then the second S1 mean signal was divided into 8 equal parts. For each part we calculated the mean square value and this value was used as a feature in the corresponding heart sound vector. In this way we calculated 8 scalar features for S1 (F5-F12), and similarly we calculated 24 scalar features for the systolic period (F13-F36), 8 scalar features for S2 (F37-F44) and 48 scalar features for the diastolic period (F45-F92). The systolic and diastolic phase components of the above first mean signal were also passed from four bandpass filters: a) a 50–250 Hz filter giving its low frequency content, b) a 100–300 Hz filter giving its medium frequency content, c) a 150–350 Hz filter giving its medium-high frequency content and d) a 200–400 Hz filter giving its high frequency content. For each of these 8 outputs, the total energy was calculated and was used as a feature in the heart sound vector (F93-F100). With the above three phases of preprocessing every heart sound signal was transformed in a heart sound vector (pattern) with dimension 1 × 100.
Finally these preprocessed data feature vectors were stored in a database table. This table had 84 records, i.e. as many records as the available heart sound signals; each record describes the feature vector of a heart sound signal and has 102 fields. Each field corresponds to one feature of the feature vector or in other words to one attribute of the heart sound. One attribute for the pattern identification code named ID (used as the primary key of this database table), one attribute named hdisease for the characterization of the specific heart sound signal as MR or AS and 100 attributes for the above 100 heart sound features (F1-F100).
The decision tree-based method
Relevance analysis
Before constructing and using the decision tree Classifiers a Relevance Analysis [24] of the features was performed. Relevance Analysis aims to improve the classification efficiency by eliminating the less useful (for the classification) features and reducing the amount of input data to the classification stage. For example from the previous description of the database table attributes it is obvious that the pattern identification code (primary key) is irrelevant to the classification, therefore it should not be used by the classification algorithm.
In this work we used the value of the Uncertainty Coefficient [23-25] of each of the above 100 features to rank these features according to their relevance to the classifying (dependent variable) attribute which in our case is the hdisease attribute. In order to compute the Uncertainty Coefficients, the 100 numeric attributes were transformed into corresponding categorical ones. The algorithm that has been used for optimizing this transformation for the specific classification decision is described in [23]. Then for each of these 100 categorical attributes, its Uncertainty Coefficient was calculated, as described in the following paragraphs.
Initially we have a set P of p data records (84 data records in our case). The classifying attribute (dependent variable) for this differential diagnosis problem has 2 possible discrete values: AS or MR, which define 2 corresponding subsets discrete classes Pi (i = 1, 2) of the above set P. If P contains pi records for each Pi (i = 1, 2), (p = p1 + p2) then the Information Entropy (IE) of the initial set P, which is a measure of its homogeneity concerning the classifying attribute-dependent variable (higher homogeneity corresponding to lower values of IE) is given by:
Any categorical attribute CA (from the 100 ones created via the above transformation) with possible values ca1, ca2, ... cak can be used to partition P into subsets Ca1, Ca2, ... Cak, where subset Caj contains all those records from P that have CA = caj. Let Caj contain p1j records of class P1 and p2j from class P2. The Information Entropy of the set P, after this partition, is equal to the weighted average of the information Entropies of the subsets Ca1, Ca2, ... Cak and is given by:
Therefore, the Information Entropy gained by partitioning according to attribute CA, namely the improvement in homogeneity concerning the classifying attribute-dependent variable is given by:
Gain(CA) = IE(p1, p2) - IE(CA) (3)
The Uncertainty Coefficient U (CA) for a categorical attribute CA is obtained by normalizing this Information Gain of CA so that U (CA) ranges from 0% to 100 %.
A low value of U(CA) near 0% means that there is no increase in homogeneity (and therefore in classification accuracy) if we partition the initial set according to CA therefore there is low dependence between the categorical attribute CA and the classifying attribute-dependent variable, while a high value near 100% means that there is strong relevance between the two attributes.
Construction of decision tree classifier structures
A decision tree is a class discrimination tree structure consisting of non-leaf nodes (internal nodes) and leaf nodes (final-without child nodes), [23,25,28]. For constructing a decision tree we use a training data set, which is a set of records, for which we know all feature-attributes (independent variables) and the classifying attribute (dependent variable). Starting from the root node, we determine the best test (= attribute + condition) for splitting the training data set, which created the most homogeneous subsets concerning the classifying attribute and therefore gives the highest classification accuracy. Each of these subsets can be further split in the same way etc. Each non-leaf node of the tree constitutes a split point, based on a test on one of the attributes, which determines how the data is partitioned (split). Such a test at a decision tree non-leaf node usually has exactly two possible outcomes (binary decision tree), which lead to two corresponding child nodes. The left child node inherits from the parent node the data that satisfies the splitting test of the parent node, while the right child node inherits the data that does not satisfy the splitting test. As the depth of the tree increases, the size of the data in the nodes is decreasing and the probability that this data belongs to only one class increases (leading to nodes of lower impurity concerning the classifying attribute-dependent variable). If the initial data that is inherited to the root node are governed by strong classification rules, then the decision tree is going to be built in a few steps, and the depth of the tree will be small. On the other hand, if the classification rules in the initial data of the root node are weak, then the number of steps to build the classifier will be significant and the depth of the tree will be higher.
During the construction of the tree, the goal at each node is to determine the best splitting test (= attribute + condition), which best divides the training records belonging to that leaf into most homogeneous subsets concerning the classifying attribute. The value of a splitting test depends upon how well it separates the classes. For the evaluation of alternative splitting tests in a node various splitting indexes can be used. In this work the splitting index that has been used is the Entropy Index [28]. Assuming that we have a data set P which contains p records from the 2 classes and where pj/p is the relative frequency of class j in data set P then the Entropy Index Ent(P) is given by:
Differential Diagnosis Meaning
If a split divides P into two subsets P1 and P2 where P1 contains p1 examples, P2 contains p2 examples and p1 + p2 = p, then the values of Entropy Index of the divided data is given by:
In order to find the best splitting test (= attribute + condition) for a node we examine for each attribute data set all possible splitting tests based on these attributes. We finally select the splitting test with the lowest value for the above Entsplit to split the node.
The expansion of a decision tree can continue, dividing the training set in to subsets (corresponding to new child nodes), until we have subsets-nodes with 'homogeneous' records having all the same value of the classification attribute. Although theoretically this is a possible scenario in practical situations usually leads to a decision tree structure that is over-fitted to the training data set and to the noise this data set contains. Consequently such a decision tree structure has not good generalization capabilities (= high classification accuracy for other test data sets). Stopping rules have been therefore adopted in order to prevent such an over-fitting; this approach is usually referred to as decision tree Pruning [27]. A simple stopping rule that has been examined in this work was a restriction concerning the minimum node size. The minimum node size sets a minimum number of records required per node; in our work for the pruned decision tree structure described in the Results section a node was not split if it had fewer records than a percentage of the initial training data set records (percentages 5%, 10%, 15%, and 20% were tried).
Finally the constructed Decision tree structure is used as a classifier in order to classify new data sets. In our work we used this classifier to classify both the training data set and the test data set.
Selection of training and test pattern sets
In practical situations, where the acquisition of heart sound signals for all probable cases is time consuming and almost impossible, we are very much interested in the capability of the constructed-trained decision tree structure to generalize successfully. In order to examine the generalization capabilities of the constructed decision tree structures, the complete pattern set was divided in two subsets. The first subset included 34 patterns, 17 with AS systolic murmur and 17 with MR systolic murmur (40% of each category of the heart sound patterns set) randomly selected out of each pattern category (AS and MR) of the patterns set. This subset was used as the training set. The other subset, that included the remaining 50 patterns (24 belonging to the AS class and 26 belonging to the MR class), was used as the test set. In this way the first training-test sets scheme was developed. The division of the pattern set was repeated, keeping the same proportions (40% training set – 60% test set), but using different patterns giving a second scheme. In the same way we created some more schemes with different proportions in order to examine the impact of the training and test data set size on the performance of the decision tree classifier. These schemes are presented in Table Table11.
Table 1
| Schemes | Number of records of Training dataset | Number of records of Test dataset |
| 40% a | 34 | 50 |
| 40% b | 34 | 50 |
| 50% a | 42 | 42 |
| 50% b | 42 | 42 |
| 60% a | 51 | 33 |
| 60% b | 50 | 34 |
| 70% a | 59 | 25 |
| 70% b | 59 | 25 |
| 80% a | 67 | 17 |
| 80% b | 67 | 17 |
Results
Relevance analysis
In order to investigate the relevance and the contribution to the differentiation between AS, and MR for each of the above mentioned 100 heart sound features, the Uncertainty Coefficients were calculated for each one of them considering the hdisease field as the classifying attribute. The calculation was made separately for the training data set of each of the 10 schemes outlined in Table Table11 and for each heart sound feature. Then the average value and the standard deviation of the Uncertainty Coefficient were calculated taking into account the 10 values that were calculated from these 10 schemes. The average values and the standard deviations of the Uncertainty Coefficient for all the 100 features are presented in Figure Figure2.2. Note that the most relevant features are the frequency features (i.e. E_dias_hf = High Frequency Energy in diastolic phase, E_dias_mf = Medium Frequency Energy in diastolic phase, E_sys_hf = High Frequency Energy in systolic phase, E_dias_mh = Medium High Frequency Energy in diastolic phase, etc) and the morphological features that describe the S1 (i.e. s1_1...s1_8), the S2 (i.e. s2_1...s2_8) and the systolic murmur (sys1, ... sys24). These results are compatible with our physical understanding of the problem; the AS and MR systolic murmurs have different frequency content and different envelope shape. On the contrary, in the diastolic phase there is no murmur in both diseases, therefore the diastolic phase of heart sound signals cannot contribute to the differentiation between AS and MR. Additionally the closure of Mitral valve affects the S1 and the closure of Aortic valve affects the S2.
Average values and standard deviations of the uncertainty coefficient for the 100 features regarding the disease attribute.
The standard deviation values are generally smaller that 10%, showing that the Uncertainty Coefficients calculated from each scheme separately, especially the ones of the most relevant features, are similar and consistent.
Fully expanded decision tree
According to the methodology described in the Methods section, we initially construct the decision tree structure with no restriction to the nodes (without pruning). The trainingl Workshop on Research Issues on Data Engineering (RIDE'97) Birmingham, England; 1997. Generalisation and Decision Tree Induction: Efficient Classification in Data Mining; pp. 11–120. [Google Scholar]